Lines and Angles: Definition, Types and Properties

 What are Lines?

A line is a straight one-dimensional figure, that extends in the opposite directions infinitely. A line can be horizontal or vertical. It can be drawn from left to right or top to bottom.

What are Angles?

Angles are the shape that is formed when the endpoints of two rays meet at a single point. They are measured in degrees (°) or radians. A complete rotation is equal to an angle of 360 degrees. It is represented by the symbol ‘∠’.

Types of Lines and Angles

There are various types of lines and angles in geometry based on the measurements and different scenarios. Let us learn here all those lines and angles along with their definitions.

Types of Lines

Lines are basically categorized as:

• Line segment
• Ray

Based on concepts or operations performed on lines, they are;

• Parallel Lines
• Perpendicular Lines
• Transversal

Line Segment

A line segment is a part of a line with two end-points. It is the shortest distance between two points and has a fixed length.

 

    

Ray

A ray is a part of a line, which has a starting point and extends infinitely in one direction.

    

Perpendicular Lines

When two lines form a right angle with each other, by meeting at a single point, are called perpendicular lines. In the figure, you can see, lines AB and CD are perpendicular to each other.

    

Parallel Lines

Two lines are said to be parallel when they do not meet at any point in a plane or which do not intersect each other. In the figure, lines PQ and RS are parallel to each other.

    

Transversal Line

When a line intersects two lines at distinct points, it is called a transversal. In the figure, a transversal l is intersecting two lines at point P and Q.

    

Types of Angles

Angles are basically classified as:

• Acute Angle (<90°)
• Right Angle (=90°)
• Obtuse Angle (>90°)
• Straight Angle (=180°)

And based on the relation between two angles, conceptual wise, they are;

• Supplementary Angles
• Complementary Angles
• Adjacent Angles
• Vertically Opposite Angles

Acute Angle

If the inclination between the arms is less than a right angle, it is called an acute angle.

Obtuse Angle

If the inclination between the arms is more than a right angle, it is called an obtuse angle.

Right Angle

If the arms form an angle of 90 degrees between them, it is called a right angle.

Straight Angle

If the arms form an angle of 180 degrees between them, it is called a straight angle.

Complementary Angles

Two angles which sum up to 90 degrees are called complementary angles.

    

Supplementary Angles

Two angles which sum up to 180 degrees are called supplementary angles.

    

Adjacent Angles

Two angles which have a common side and a common vertex are called adjacent angles. In the following figure, ∠α and ∠β are adjacent angles.

    

Vertically Opposite Angles

Two angles which are formed, opposite to each other, when two lines intersect at a common point or vertex, are called vertically opposite angles. In the figure, given below;

    

∠POR = ∠SOQ and ∠POS = ∠ROQ

Properties of Lines and Angles

Similar to other shapes and sizes in geometry, lines and angles also have their own properties. Let us see what are they.

Properties of Lines

• Collinear points are a set of three or more points which lie on the same line.
• The points which do not lie on the same line are called non-collinear points.

Note: Three points can be either collinear or non-collinear, but not both together at the same time.

Properties of Angles

• An angle is a figure in which two rays emerge from a common point. This point is called the vertex of the angle and the two rays forming the angle are called its arms or sides.
• An angle which is greater than 180 degrees but less than 360 degrees is called a reflex angle.
• If two adjacent angles add up to 180 degrees, they form a linear pair of angles. In the following figure, ∠a and ∠b forms a linear pair.

  

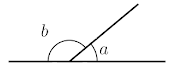
• When two lines intersect each other, the two opposite pairs of angles formed are called vertically opposite angles. In the following figure, ∠A and ∠B are vertically opposite angles. Another pair is ∠C and ∠D.