Pythagoras Theorem

Trigonometry

Trigonometry is the branch of mathematics which literally consists of three words. Tri referring to three, gono meaning angle and metry which means measurement. Hence, trigonometry refers to the measurement of triangles. We shall only deal with right- angled triangles.

Right-angled triangle

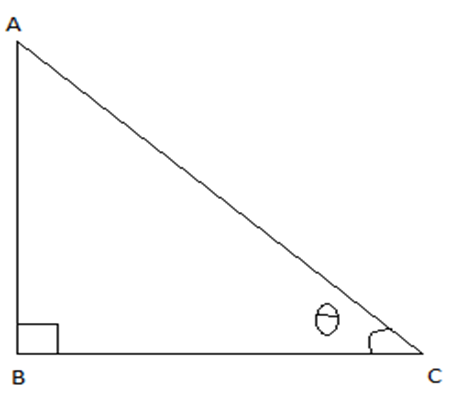
A triangle having one angle 90˚ is known as right-angled triangle. The side opposite to right angle is called hypotenuse. It is denoted by ‘h’.

                                                                                                                                                   In the figure, AC is the hypotenuse. 

Reference Angle

An angle that is taken into consideration before finding out perpendicular and base in right-angled triangle is known as Reference angle. It is usually denoted by Greek Alphabet. The side in front of the reference angle is called perpendicular and the remaining side is called base. Perpendicular and base are denoted by ‘p’ and ‘b’ respectively.

So, in short, p, b and h are the elements of right-angled triangle.

 From figure,           AB = Perpendicular (p)

                                BC = Base (b)

                                AC = Hypotenuse (h)

 Pythagoras Theorem

In any right-angled triangle the squares made on the hypotenuse is always equal to the sum of the squares made on the remaining two sides.

Mathematically, h² = p² + b²

Converse of Pythagoras Theorem

Converse of Pythagoras Theorem states that if Pythagoras Theorem is h² = p² + b² holds true then the triangle must be a right-angled triangle.

                                                                                            

Here in       DEF,

DF = 10 cm, DE = 8 cm and FE = 6 cm.

We have to see whether the triangle is right-angled triangle.

So, for DEF to be a right-angled triangle,

(DF)² = (DE)² + (EF)²            {DF is the longest side so it is considered hypotenuse}

Or,       (10)² = (8)² + (6)²

Or,       100 = 64 + 36

Or,       100 = 100 (true)

Since, Pythagoras theorem holds DEF is a right-angled triangle.                               

1.  Find out p, b and h from the following right-angled triangle with the given angle of reference (i) R = θ be the reference angle.      (ii) P = α be the reference angle.

                                                                                        

Here, in right-angled ∆PQR, <Q = 90˚

(i).  <R = θ is the angle of reference,

Then,   RP = hypotenuse (h)

            PQ = perpendicular (p)

            RQ = base (b)

Again,

(ii).  <P = α be the reference angle

Then,   RP = hypotenuse (h)

            RQ = Perpendicular (p)

            PQ = base (b)

2.  Find the missing side from the right-angled triangle given below.

                                                                        

Here, in right-angled triangle ∆ABC,

<B = 90˚, AB = 5 cm, AC = 13 cm, BC =?

We know,

In right-angled ∆ABC

h² = p² + b²

so,        (AC)² = (AB)² + (BC)²

or,        (13)² = (5)² + (BC)²

or,        169 – 25 = (BC)²

or,        (BC)² = 144

or,        (BC)² = 12²

or,        BC = 12

hence, BC is 12 cm

3.  Find the missing side from the right-angled triangle given below.

                                                                                            

In right-angled ∆PQR,

(PR)² = (PQ)² + (QR)²

Or,       (PR)² = (3)² + (4)²

Or,       (PR)² = 9 + 16

Or,       (PR)² = 25

Or,       (PR)² = (5)²

            PR = 5 cm

Now, in right-angled ∆PSR

            (SR)² = (PS)² + (PR)²

Or,       (SR)² = (12)² + (5)²

Or,       (SR)² = 144 + 25

Or,       (SR)² = 169

Or,       (SR)² = (13)²

            SR = 13 cm